|
|
|
|
|
|
1.
|
Examine the information above.
On the right, list the things you expect to learn from this lesson.
Review the vocabulary words
and look for them as you work through the lesson. You will be tested on them
later.
|
|
|
The marginal product of labor is the increase in output
added by the last unit of labor. In
Section 1, we identified how producers respond to a change in price. The law of supply states that
producers will offer more goods as the price goes up and fewer as the price falls. In this section,
we will explain how a supplier decides how much to produce.
Consider a firm that
produces beanbags The firm’s factory has one sewing machine and one pair of scissors. The
firm’s inputs are workers and materials, including cloth, thread, and beans. Assume that each
beanbag requires the same amount of materials. As the number of workers increases, what happens to
the quantity of beanbags produced? | Labor and
Output
One of the basic
questions any business owner has to answer is how many workers to hire. To answer this question,
owners have to consider how the number of workers they hire will affect their total production. For
example, at the beanbag factory, one worker can produce four beanbags per hour. Two workers can make
a total of ten bags per hour, and three can make a total of seventeen beanbags an hour. As new
workers join the company, total output increases. After the seventh worker is hired, production peaks
at 32 beanbags per hour. When the firm hires the eighth worker, however, total output drops to 31
bags per hour.
Figure 5.6 shows the relationship between labor, measured by the number of
workers in the factory, and the number of beanbags produced. | | |
|
|
|
2.
|
Why does the marginal product
of labor decrease with more than four workers in this
example?
a. | They did not hire enough
workers | c. | They do not have
enough material to increase production | b. | Production is limited by the equipment needed to increase
production | d. | They need to increase wages to
increase production |
|
|
|
3.
|
At what point does an increase
in hiring actually decrease the number of beanbags produced?
a. | 4
workers | c. | 7
workers | b. | 6 workers | d. | 8 workers |
|
|
|
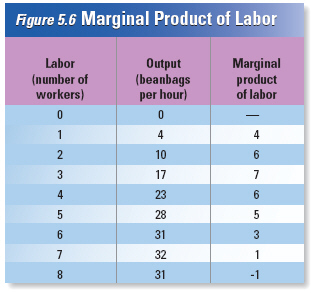
Marginal
Product of Labor
The
third column of Figure 5.6 shows the
marginal product of labor, or the change in
output
from hiring one more worker. This
is called the marginal product because it
measures the change
in output at the
margin, where the last worker has been
hired or fired. | The first worker
to be hired produces
four bags an hour, so her marginal product
is four bags. The second worker
raises total
output from four bags an hour to ten, so her
marginal product of labor is six.
Looking
at this column, we see that the marginal
product of labor increases for the first
three
workers, rising from four to seven. | | |
|
|
|
4.
|
How many workers produces the
highest marginal product of labor?
|
|
|
5.
|
Which statement is
true?
a. | Hirering more workers always results
in more production | c. | Hiring more
workers never results in more production | b. | Hiring more workers does not necessarily result in more
production | d. | There is no way to tell how many
workers will increase production |
|
|
|
Increasing
Marginal Returns
The
marginal product of labor increases for the first three workers because there are three tasks
involved in making a beanbag. Workers cut and sew cloth into the correct shape, stuff it with beans,
and sew the bag closed. In our example, a single worker performing all these tasks would only produce
four bags per hour. Adding a second worker would allow each worker to specialize in one or two tasks.
If each worker focuses on only one part of the | process, she will waste less time
switching between tasks and will become more skillful at her assigned tasks. In other words,
specialization increases output per worker, so the second worker adds more to output than the first.
The firm enjoys increasing marginal
returns.
In our example, there are benefits from specialization for the first three
workers. The firm enjoys a rising marginal product of labor for the first three
workers. | | |
|
|
|
6.
|
How many tasks are required to
produce a bean bag?
|
|
|
7.
|
What effect does specialization
have on the production of bean bags?
a. | it increases the productivity of the
workers | c. | it decreases the
marginal productivity no matter how many workers are hired | b. | it decreases the productivity of the
workers | d. | it has no effect on
productivity |
|
|
|
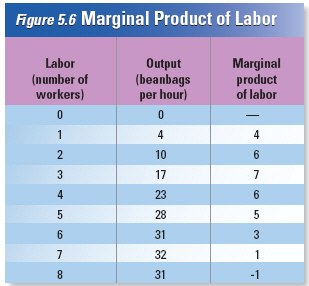
Diminishing
Marginal Returns
When
the fourth through the seventh workers are hired, the marginal product of labor is still positive.
Each new worker still adds to total output. However, the marginal product of labor shrinks as each
worker joins the company. The fourth worker increases output by six bags, while the seventh increases
output by only one bag. Why?
After the beanbag firm hires its first three workers, one for
each task, the benefits of specialization end. At that point, adding more workers increases total
output, but at a decreasing rate. This situation is known as diminishing marginal returns. A
firm with diminishing marginal returns of labor will produce less and less output from each
additional unit of labor added to the mix.
The firm suffers from diminishing marginal returns
from labor because its workers must work with a limited amount of capital. Remember that capital is
any human-made resource that is used to produce other goods. In this example, capital is represented
by the factory’s single sewing machine and pair of scissors.
| When there are
three workers, but only one needs to use the sewing machine, this worker will never have to wait to
get to work. When there are more than three workers, the factory will assign more than one to
work at the sewing machine. While one is working, the other will have to wait. She may be able to
help cut fabric or stuff bags in the meantime, but every bag must be sewn up at some point, so she
cannot greatly increase the speed of the production process.
The problem gets worse as more
workers are hired and the amount of capital remains constant. Wasted time waiting for the sewing
machine or scissors means that additional workers will add less and less to total output at the
factory.
Negative Marginal Returns
As the table in Figure 5.6 shows,
adding the eighth worker at the beanbag factory can actually decrease output by one bag. At this
stage, workers get in each other’s way and disrupt the production process, so overall output
decreases. Of course, few companies ever hire so many workers that their marginal product of labor
becomes negative | | |
|
|
|
8.
|
At that point does adding more
workers increases total output, but at a decreasing rate.
a. | 4
workers | c. | 7
workers | b. | 5 workers | d. | 8 workers |
|
|
|
9.
|
What do they call it when you
add more workers that increases total output but at a decreasing rate?
a. | productivity
enhancement | c. | increasing
marginal returns | b. | specialization | d. | diminishing marginal returns |
|
|
|
10.
|
What is the biggest impediment
to specialization and increasing marginal productivity?
a. | land | c. | capital | b. | labor | d. | finance |
|
|
|
 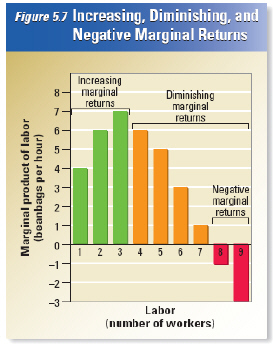
Labor has increasing and then diminishing
marginal returns.
|
|
|
11.
|
What is the marginal product of
labor when the factory currently employs five workers?
|
|
|
12.
|
Look at the chart on the right.
Remember that labor is expensive. How many workers would you hire to maximize specialization and
productivity?
|
|
|

Production
Costs
Paying workers and
purchasing capital are all costs of producing goods. Economists divide a producer? ’s costs
into two categories: fixed costs and variable costs.
|
|
|
13.
|
Firms must separate fixed costs
from variable costs to determine whether or not to
produce at a given market price. Why are some
employees considered variable costs?
a. | They are essential to running the
company and must be paid no matter what | c. | They are always full time employees | b. | They are non-essential and the company can do without them
if necessary. Their usefulness varies from time to time | d. | They do work essential for the company to make a
profit |
|
|
|
14.
|
Rent and utilities are
considered
a. | fixed
costs | c. | marginal
expenditures | b. | variable costs | d. | capital |
|
|
|
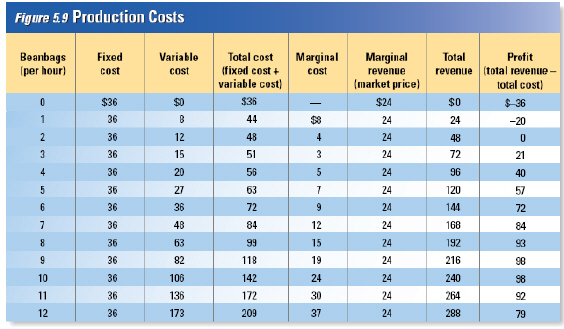 Firms consider a variety of costs when deciding how
much to produce. Firms consider a variety of costs when deciding how
much to produce. Fixed
Costs
A fixed cost
is a cost that does not change, no matter how much of a good is produced. Most fixed costs
involve the production facility, the cost of building and equipping a factory, office, store, or
restaurant. Examples of fixed costs include rent, machinery repairs, property taxes on a factory, and
the salaries of workers who keep the business running even when production temporarily
stops.
| Variable
Costs
Variable costs
are costs that rise or fall depending on the quantity produced. They include the costs of raw
materials and some labor. For example, to produce more beanbags, the firm must purchase more beans
and hire more workers to stuff the beanbags. If the company wants to produce less and cut costs, it
can stop buying beans or have some workers work fewer hours a week. The cost of labor is a variable
cost because it changes with the number of workers, which changes with the quantity produced.
Electricity and heating bills are also variable costs, because the company can cut off heat and
electricity for the factory and its machines when they are not in use. | | |
|
|
|
15.
|
What is the total cost of
producing 7 bean bags?
|
|
|
16.
|
How many bean bags will give
you the greatest profit?
|
|
|
17.
|
Would you rather take in $216
or $240 in total revenue?
a. | $240 because you make more
profit | c. | Neither is enough to sustain the
business | b. | $216 because costs are not as high | d. | It doesn’t matter because they both yield the same amount of
profit |
|
|
|
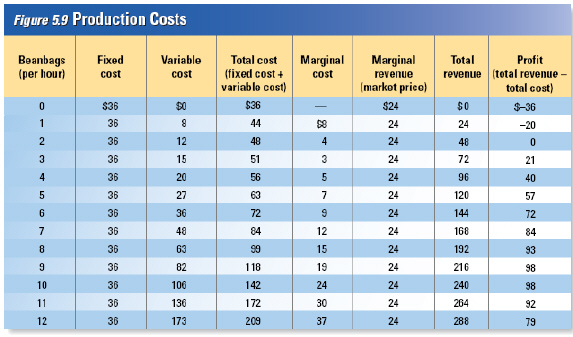
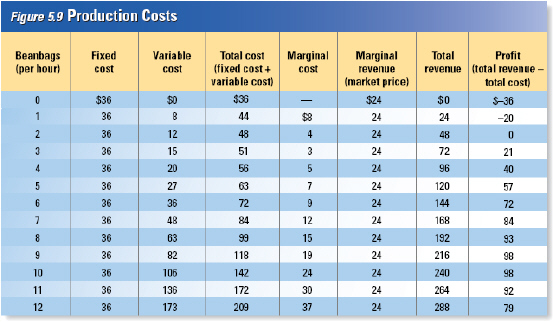 Total
Cost
Figure 5.9 shows
some cost data for the firm that produces beanbags. The firm has a factory that is fully equipped to
produce beanbags. How does the cost of producing beanbags change as the output increases?
In
our example, the fixed costs are the costs of the factory building and all the machinery and
equipment inside. As shown in the second column in Figure 5.9, the fixed costs are $36.00 per
hour.
Variable costs include the cost of beans, fabric, and most of the workers hired to
produce the beanbags. As shown in the third column, variable costs rise with the number of beanbags
produced. Fixed costs and variable costs are added together to find total cost. Total cost is
shown in the fourth column.
 | Marginal
Cost
If we know the
total cost at several levels of output, we can determine the marginal cost of production at
each level. Marginal cost is the additional cost of producing one more unit.
As shown in
Figure 5.9, even if the firm is not producing a single beanbag, it still must pay $36.00 an hour for
fixed costs. If the firm decides to produce just one beanbag an hour, its total cost rises $8.00 from
$36.00 to $44.00 an hour. The marginal cost of the first beanbag is $8.00.
For the first three
beanbags, the marginal cost falls as output increases. The marginal cost of the second beanbag is
$4.00, and the marginal cost of the third beanbag is $3.00. Each additional beanbag is cheaper to
make because of increasing marginal returns resulting from specialization.
With the fourth
beanbag, the marginal cost starts to rise. The marginal cost of the fifth per hour is $7.00, the
sixth costs $9.00, and the seventh, $12.00. The rising marginal cost reflects diminishing returns to
labor. The benefits of specialization are exhausted at three beanbags per hour, and diminishing
returns set in as more and more workers share a fixed production facility. | | |
|
|
|
18.
|
At what point does the marginal
cost of producing beanbags begin to rise?
a. | 3 bags | c. | 6 bags | b. | 4 bags | d. | 8 bags |
|
|
|
19.
|
So what does the marginal cost
of production tell the businessman?
a. | The cost in production by adding
additional workers | c. | Whether or not to
increase supply | b. | The total revenue taken in | d. | The projected demand for his
products |
|
|
|
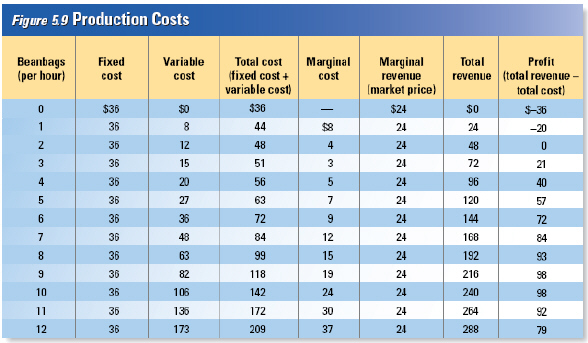 Setting Output Setting Output
Behind all of the decisions about how many workers
to hire is the firm’s basic goal: to maximize profits. Profit is defined as total revenue minus
total cost. As you read in Chapter 4, a firm’s total revenue is the money the firm gets by
selling its product. Total revenue is equal to the price of each good multiplied by the number of
goods sold. Figure 5.9 shows total revenue when the price of a beanbag is $24.00. To find the level
of output with the highest profit, we look for the biggest gap between total revenue and total cost.
The gap is biggest and profit is highest when the firm makes 9 or 10 beanbags per hour. At this rate,
the firm can expect to make a profit of $98.00 an hour.
|
|
|
20.
|
Why wouldn’t you make, at
least, some profit by producing 2 beanbags?
a. | Because there is not enough total
revenue | c. | because total
costs equal total revenue | b. | Because fixed costs are higher than variable
costs | d. | because total revenue is only
$10 |
|
|
|
21.
|
If you don’t produce any
beanbags, why are you loosing money?
a. | Because fixed costs still have to be
paid | c. | Because there are not enough
workers | b. | Because variable costs are not high enough | d. | Because you still have to pay the fixed
costs |
|
|
|
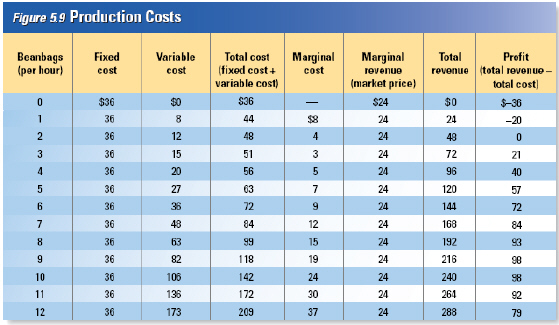 Marginal
Revenue and Marginal Cost
Another way to find the best level of output is to find the output level where
marginal revenue is equal to marginal cost. Marginal revenue is the additional income from
selling one more unit of a good. If the firm has no control over the market price, marginal revenue
equals the market price. Each beanbag sold at $24.00 increases the firm’s total revenue by
$24.00, so marginal revenue is $24.00.
According to the table, price equals marginal cost
with 10 beanbags, so that’s the quantity that maximizes profit at $98 an hour.
To
understand how an output of 10 beanbags maximizes the firm’s profits, suppose that the firm
picked a different level of output. If the firm made only 4 beanbags per hour, is it making as much
money as it can? From Figure 5.9, we know that the marginal cost of the fifth beanbag is $7.00.
The market price for a beanbag is $24.00, so the marginal revenue from that beanbag is $24.00. The
$17.00 difference between the marginal revenue and marginal cost represents pure profit for the
company from making and selling the fifth beanbag. The company should increase its production to five
beanbags an hour to capture that profit on the fifth beanbag.
| If we do the same calculations for a sixth
beanbag, we find that the company can capture a profit of $15.00 by producing the sixth beanbag per
hour. The price of the seventh beanbag is $12.00 higher than its marginal cost, so that beanbag earns
an additional $12.00 in profit for the company. The profit is available any time the company receives
more for the last beanbag than it cost to produce. Any rational entrepreneur would take this
opportunity to increase profit.
Now suppose that the firm is producing so many beanbags an
hour that marginal cost is higher
than price. If the firm produces eleven beanbags an hour, it receives $24.00 for that eleventh
beanbag, but the $30.00 cost of that beanbag wipes out the profit. The firm actually loses $6.00 on
the sale of the eleventh beanbag. Because marginal cost is increasing, and price is constant in this
example, the losses would get worse at higher levels of output. The company would be better off
producing less and keeping costs down.
The ideal level of output is where marginal revenue
(price) is equal to marginal cost. Any other quantity of output would generate less
profit.
| | |
|
|
|
22.
|
Why would we try to find the
output level of marginal revenue that is equal to marginal cost?
a. | to find the best level of
input | c. | to determine the price of
products | b. | to find the best level of output | d. | to determine the cost of capital |
|
|
|
23.
|
What is marginal
revenue?
a. | the difference between capital and
labor | c. | the additional cost of selling all
goods | b. | the additional cost from selling one more unit of a
good | d. | the additional income from selling one more unit of a
good |
|
|
|
24.
|
According to the table, price
equals marginal cost with _____ beanbags, so that’s the quantity that maximizes profit at $98
an hour.
|
|
|
25.
|
Look at the chart above. Is it
possible for this company to produce so many beanbags that they loose money by producing them?
a. | yes | c. | the chart does not show
this | b. | no | d. | Silly, it is obvious that the more
beanbags you produce the more money you will make |
|
|
|
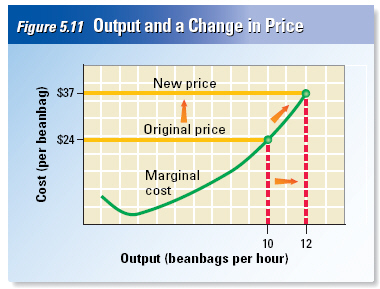
Responding
to Price Changes
What
would happen if the price of a beanbag rose from $24.00 to $37.00? Thinking at the margin, we would
predict that the firm would increase production to twelve beanbags per hour. That’s the
quantity at which the marginal cost is equal to the new, higher price. At the original price of
$24.00, the firm would not produce more than ten beanbags, according to
Figure 5.11. When the
price rises to $37.00, marginal revenue soars above marginal cost at that output level. Raising
production to twelve beanbags an hour would allow the firm to capture profits on the eleventh and
twelfth beanbags. |
This example shows the law of supply in
action. An increase in price
from $24.00
to $37.00 causes the firm to increase the
quantity supplied from ten to
twelve
beanbags an hour.
| | |
|
|
|
26.
|
If the price of beanbags
remains at $24 the company will loose money by increasing supply (production) What happens if they
increase the price from $24 to $37
a. | the company will still loose
money | c. | the companies profits will remain
the same | b. | the companies profits will go up | d. | increasing price has no effect on
supply |
|
|
|
27.
|
This chart is an illustration
of the law of _____ .
a. | supply | c. | equilibrium | b. | demand | d. | falling revenues |
|
|
|
 The Shutdown Decision The Shutdown Decision
Consider the problems faced by a factory
that is losing money. The factory is producing at a level of output at which marginal revenue
is equal to marginal cost. As you have read, this is the most profitable level of output. However,
the market price is so low that the factory’s total revenue is still less than its total cost,
and the firm is losing money. Should this factory continue to produce goods and lose money, or should
its owners shut the factory down? This may seem like a silly question. In fact, there are times when
keeping a money-losing factory open is the best choice. The firm should keep the factory open if the
total revenue from the goods and services the factory produces is greater than the cost of keeping it
open.
For example, if the price of beanbags drops to $7, and the factory produces at the
profit-maximizing level of five beanbags per hour, the total revenue of the business is $35 per hour.
Weigh this against the factory? ’s operating cost, or the cost of operating the
facility. The operating cost includes the variable costs the owners must pay to keep the factory
running, but not the fixed costs, which the owners must pay whether the factory is open or
closed.
According to Figure 5.9, if the factory produces five beanbags, the variable cost is
$27 per hour. Therefore, the benefit of operating the facility (total revenue of $35) is greater than
the variable cost ($27), so it makes sense to keep the facility running.
Consider the effects
of the other choice. If the firm were to shut down the factory, it would still have to pay all of its
fixed costs. The factory? ’s total revenue would be zero because it would be producing nothing
for sale. Therefore, the firm would lose an amount of money equal to its fixed costs.
For this
beanbag factory, the fixed costs equal $36 per hour, so the factory would lose $36 for each hour it
is closed. If the factory were to keep producing five beanbags per hour, its total cost would be $63
($36 in fixed costs plus $27 in variable costs) per hour, but it would lose only $28 ($63 in total
cost minus $35 in revenue) for each hour it is open. The factory would lose less money while
producing because the total revenue ($35) would exceed the variable costs ($27), leaving $8 to cover
some of the fixed costs. Although the factory would lose money in either situation, it would lose
less money by continuing to produce and sell beanbags.
How long will a business continue to
operate a factory at a loss before it decides to replace the facility? The firm will build a new
factory and stay in the market only if the market price of beanbags is high enough to cover all the
costs of production, including the cost of building a new factory.
|
|
|
28.
|
When should a company keep its
factory open even though it is loosing money?
a. | You will make more profits once you
hire more workers and increase production of beanbags | c. | To benefit the workers who would loose their jobs if the factory
closed | b. | The firm should keep the factory open if the total revenue from the goods and
services the factory produces is lower than the cost of keeping it open.
| d. | The firm should keep the factory open if the total revenue
from the goods and services the factory produces is greater than the cost of keeping it open.
|
|
|
|
29.
|
Even though you may shut down
an unprofitable factory, you would still have to pay the
a. | variable
costs | c. | supply
costs | b. | labor costs | d. | fixed costs |
|
|
|
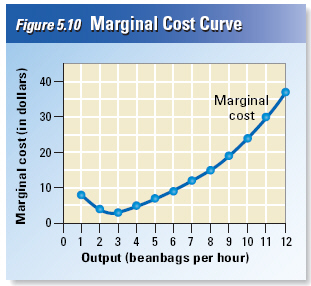
For
most firms, the marginal cost of production falls as output rises from zero, but eventually begins to
rise.
|
|
|
30.
|
How many beanbags an hour
should this firm make to produce at the lowest possible marginal cost?
|
|
|
a. | fixed cost
| f. | increasing marginal
returns | b. | marginal cost | g. | operating cost | c. | marginal product of labor | h. | diminishing marginal returns | d. | marginal revenue | i. | variable cost | e. | total cost |
|
|
|
31.
|
a level of production in
which the marginal product of labor decreases as the number of workers
increases
|
|
|
32.
|
a cost that does not change,
no matter how much of a good is produced
|
|
|
33.
|
the change in output from
hiring one additional unit of labor
|
|
|
34.
|
fixed costs plus variable
costs
|
|
|
35.
|
a cost that rises or falls
depending on how much is produced
|
|
|
36.
|
the additional income from
selling one more unit of a good; sometimes equal to price
|
|
|
37.
|
a level of production in
which the marginal product of labor increases as the number of workers
increases
|
|
|
38.
|
the cost of operating a
facility, such as a store or factory
|
|
|
39.
|
the cost of producing one
more unit of a good
|